Los vectores son una forma de almacenar datos que permiten contener una serie de valores del mismo tipo, cada uno de los valores contenidos tiene una posición asociada que se usará para accederlos. Está posición o índice será siempre un número entero positivo.
En C la cantidad de elementos que podrá contener un vector es fijo, y en principio se define cuando se declara el vector. Los vectores se pueden declarar de la siguiente forma:
tipo_elemento nombre[largo];
Esto declara la variable nombre como un vector de tipo_elementos que podrá contener largo cantidad de elementos, y cada uno de estos elemento podrá contener un valor de tipo tipo_elemento.
Por ejemplo:
double valores[128];
En este ejemplo declaramos un vector de 128 elementos del tipo double, los índices de los elementos irían entre 0 (para el primer elemento y 127 para el último).
De la misma forma que con las otras declaraciones de variables que hemos visto se le puede asignar un valor iniciar a los elementos.
O también se pueden declarar:
tipo_elemento nombre[largo]={valor_0, valor_1, valor_2};
En caso estamos asignadole valores a los primeros 3 elementos del vector nombre. Notar que largo debe ser mayor o igual a la cantidad de valores que le estamos asignando al vector, en el caso de ser la misma cantidad no aporta información, por lo que el lenguaje nos permite escribir:
tipo_elemento nombre[]={valor_0, valor_1, valor_2};
Que declarará nombre como el vector de largo 3.
Para acceder a un elemento accederemos a través de su posición. Es decir:
tipo_elemento elemento;
...
elemento = nombre[2];
Asumiendo que tenemos el vector anterior definido estaríamos guardando valor_2 en elemento.
Veamos algunos ejemplos:
/*
* Ejemplo : El producto escalar de dos vectores
*/
#include <stdio.h>
double producto_escalar(double v1[], double v2[], int d);
int main()
{
const int largo = 3;
double vector_1[] = {5,1,0};
double vector_2[] = {-1,5,3};
double resultado = producto_escalar(vector_1, vector_2, largo);
// imprime el resultado
printf("(%f, %f, %f) . (%f, %f, %f) = %f\n",
vector_1[0], vector_1[1], vector_1[2],
vector_2[0], vector_2[1], vector_2[2],
resultado);
return 0;
}
/* producto escalar entre dos vectores */
double producto_escalar(double v1[], double v2[], int d)
{
double resultado = 0;
int i;
for (i=0; i < d; i++) {
resultado += v1[i] * v2[i];
}
return resultado;
}
En el ejemplo anterior usamos los vectores de C para representar vectores matemáticos y calcular el producto escalar entre ellos. Una peculiaridad que se puede notar es que al recibir un arreglo en una función no se especifica el largo, volveremos a esto en un capítulo posterior.
Otra función clásica es la búsqueda de un máximo o mínimo, que podemos escribirla de la siguiente manera:
int buscar_maximo(double valores[], int num_valores)
{
int maximo_pos = 0;
for (int i = 1; i < num_valores; i++) {
if (valores[i] > valores[maximo_pos]) {
maximo_pos = i;
}
}
return maximo_pos;
}
Otro ejemplo sencillo, calcular el promedio de los valores.
double promedio(double valores[], int largo)
{
double suma=0;
for (int i=0;i<largo;i++) {
suma+=valores[i];
}
return suma/largo;
}
Cuando una función recibe un vector por parámetro y cambia su contenido y el cambio es permanente (se ve aún fuera de la función). Esto puede parecer extraño después del énfasis que pusimos en resaltar que todos los parámetros de una función se reciben por valor, pero se aclarará en el siguiente capitulo.
Mientras tanto usemos esto para definir una función que le aplique otra función que recibe por parámetro a cada elemento del vector, guardando el resultado en el mismo vector y una llamada de ejemplo a esta.
void cuadrados(double vector[], int largo)
{
for (int i=0;i<largo;i++) {
vector[i]=cuadrado(vector[i]);
}
}
...
double cuadrado(double valor) {
return valor*valor;
}
...
cuadrados(elementos,num_elem);
...
De la misma forma que venimos usando vectores de tipos básicos, podemos tener vectores de vectores, estos se declaran de la siguiente forma:
int matriz[3][7];
int tabla[3][4]={ { 1, 2, 3, 4},
{ 5, 6, 7, 8}, /* los espacios y saltos de líneas no son tomados en cuenta */
{ 9,10,11,12} };
double v[2][2][2];
...
printf("tabla[0][1]: %i\n", tabla[0][3]); // Imprime 4
printf("tabla[2][0]: %i\n", tabla[2][0]); // Imprime 9
...
En este ejemplo tabla es un vector de longitud 3, cuyos elementos son vectores de longitud 4 de elementos de tipo int.
En resumen, suponiendo que v[n] es un vector de cualquier tipo de dato con n cantidad de posiciones, al vector v se le aplican las siguientes reglas:
- La primera posición siempre será v[0]
- La última posición es v[n-1]
- En versiones previas a C99 n es una constante definida antes de la declaración de v[n]+
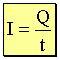
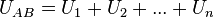
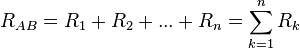
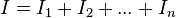
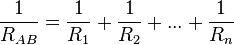
y 
o delta respectivamente. Este tipo de asociaciones son comunes en las cargastrifásicas. Las ecuaciones de equivalencia entre ambas asociaciones vienen dadas por el teorema de Kennelly:
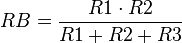
o también 
