Intensidad de corriente | |||||
Intensidad de Corriente eléctrica. La corriente eléctrica es la circulación de cargas eléctricas en un circuito eléctrico.
La intensidad de corriente eléctrica(I) es la cantidad de electricidad o carga eléctrica(Q) que circula por un circuito en la unidad de tiempo(t). Para denominar la Intensidad se utiliza la letra I y su unidad es el Amperio(A).
Ejemplo: I=10A
La intensidad de corriente eléctrica viene dada por la siguiente fórmula:
| |||||
| |||||
Donde:
I: Intensidad expresada en Amperios (A) Q: Carga eléctrica expresada en Culombios (C) t: Tiempo expresado en segundos (seg.) Habitualmente en vez de llamarla intensidad de corriente eléctrica, se utilizan indistintamente los términos: intensidad o corriente. resistencia equivalente
Asociación en serie: Se denomina resistencia equivalente de una asociación respecto de dos puntos A y B, a aquella que conectada a la misma diferencia de potencial, UAB, demanda la misma intensidad, I (ver figura 4). Esto significa que ante las mismas condiciones, la asociación y su resistencia equivalente disipan la misma potencia.
Dos o más resistencias se encuentran conectadas en serie cuando al aplicar al conjunto una diferencia de potencial, todas ellas son recorridas por la misma corriente.
Para determinar la resistencia equivalente de una asociación serie imaginaremos que ambas, figuras 4a) y 4c), están conectadas a la misma diferencia de potencial, UAB. Si aplicamos la segunda ley de Kirchhoff a la asociación en serie tendremos:
Aplicando la ley de Ohm:
En la resistencia equivalente:
Finalmente, igualando ambas ecuaciones se obtiene que:
Y eliminando la intensidad:
Por lo tanto, la resistencia equivalente a n resistencias montadas en serie es igual a la sumatoria de dichas resistencias.
Asociación en paralelo
Dos o más resistencias se encuentran en paralelo cuando tienen dos terminales comunes de modo que al aplicar al conjunto una diferencia de potencial, UAB, todas las resistencias tienen la misma caída de tensión, UAB.
Para determinar la resistencia equivalente de una asociación en paralelo imaginaremos que ambas, figuras 4b) y 4c), están conectadas a la misma diferencia de potencial mencionada, UAB, lo que originará una misma demanda de corriente eléctrica, I. Esta corriente se repartirá en la asociación por cada una de sus resistencias de acuerdo con la primera ley de Kirchhoff:
Aplicando la ley de Ohm:
En la resistencia equivalente se cumple:
Igualando ambas ecuaciones y eliminando la tensión UAB:
De donde:
Por lo que la resistencia equivalente de una asociación en paralelo es igual a la inversa de la suma de las inversas de cada una de las resistencias.
Existen dos casos particulares que suelen darse en una asociación en paralelo:
Asociación mixta
En una asociación mixta podemos encontrarnos conjuntos de resistencias en serie con conjuntos de resistencias en paralelo. En la figura 5 pueden observarse tres ejemplos de asociaciones mixtas con cuatro resistencias.
A veces una asociación mixta es necesaria ponerla en modo texto. Para ello se utilizan los símbolos "+" y "//" para designar las asociaciones serie y paralelo respectivamente. Así con (R1 + R2) se indica que R1 y R2 están en serie mientras que con (R1//R2) que están en paralelo. De acuerdo con ello, las asociaciones de la figura 5 se pondrían del siguiente modo:
Para determinar la resistencia equivalente de una asociación mixta se van simplificando las resistencias que están en serie y las que están en paralelo de modo que el conjunto vaya resultando cada vez más sencillo, hasta terminar con un conjunto en serie o en paralelo. Como ejemplo se determinarán las resistencias equivalentes de cada una de las asociaciones de la figura 5:
Desarrollando se obtiene:
Asociaciones estrella y triángulo:Teorema de Kennelly
Pueden observarse respectivamente las asociaciones estrella y triángulo, también llamadas
 y y  o delta respectivamente. Este tipo de asociaciones son comunes en las cargastrifásicas. Las ecuaciones de equivalencia entre ambas asociaciones vienen dadas por el teorema de Kennelly: o delta respectivamente. Este tipo de asociaciones son comunes en las cargastrifásicas. Las ecuaciones de equivalencia entre ambas asociaciones vienen dadas por el teorema de Kennelly:
El valor de cada una de las resistencias en estrella es igual al cociente del producto de las dos resistencias en triángulo adyacentes al mismo terminal entre la suma de las tres resistencias en triángulo.
El valor de cada una de las resistencias en triángulo es igual la suma de las dos resistencias en estrella adyacentes a los mismos terminales más el cociente del producto de esas dos resistencias entre la otra resistencia.
Asociación puente
Si en una asociación paralelo de series como la mostrada en la figura 5b se conecta una resistencia que una las dos ramas en paralelo, se obtiene una asociación puente como la mostrada en la figura 7.
La determinación de la resistencia equivalente de este tipo de asociación tiene sólo interés pedagógico. Para ello se sustituye bien una de las configuraciones en triángulo de la asociación, la R1-R2-R5 o la R3-R4-R5 por su equivalente en estrella, bien una de las configuraciones en estrella, la R1-R3-R5 o la R2-R4-R5 por su equivalente en triángulo. En ambos casos se consigue transformar el conjunto en una asociación mixta de cálculo sencillo. Otro método consiste en aplicar una fem (E) a la asociación y obtener su resistencia equivalente como relación de dicha fem y la corriente total demandada (E/I).
El interés de este tipo de asociación está en el caso en el que por la resistencia central, R5, no circula corriente o R4, en función de las otras tres. En ello se basan los puentes de Wheatstone y de hilo para la medida de resistencias con precisión.
Potencia:
Una resistencia disipa en calor una cantidad de potencia cuadráticamente proporcional a la intensidad que la atraviesa y a la caída de tensión que aparece en sus bornes.
Comúnmente, la potencia disipada por una resistencia, así como la potencia disipada por cualquier otro dispositivo resistivo, se puede hallar mediante:
A veces es más cómodo usar la ley de Joule para el cálculo de la potencia disipada, que es:
Observando las dimensiones del cuerpo de la resistencia, las características de conductividad de calor del material que la forma y que la recubre, y el ambiente en el cual está pensado que opere, el fabricante calcula la potencia que es capaz de disipar cada resistencia como componente discreto, sin que el aumento de temperatura provoque su destrucción. Esta temperatura de fallo puede ser muy distinta según los materiales que se estén usando. Esto es, una resistencia de 2 W formada por un material que no soporte mucha temperatura, estará casi fría (y será grande); pero formada por un material metálico, con recubrimiento cerámico, podría alcanzar altas temperaturas (y podrá ser mucho más pequeña).
El fabricante dará como dato el valor en vatios que puede disipar cada resistencia en cuestión. Este valor puede estar escrito en el cuerpo del componente o se tiene que deducir de comparar su tamaño con los tamaños estándar y su respectivas potencias. El tamaño de las resistencias comunes, cuerpo cilíndrico con 2 terminales, que aparecen en los aparatos eléctricos domésticos suelen ser de 1/4 W, existiendo otros valores de potencias de comerciales de ½ W, 1 W, 2 W, etc.
Pseudocodigo: |
martes, 19 de mayo de 2015
EVALUACIÓN PERMANENTE 4
EVALUACIÓN PERMANENTE 3
1) Hacer un algoritmo donde se pueda escoger 3 opciones: la primera que calcule el área de un cuadrado, segundo el área total de un cubo y tercero el área de un triángulo:
Pseudocódigo:
Compilando:
EVALUACIÓN PERMANENTE 2 - Electricidad
ELECTRICIDAD
. Es el conjunto de fenómenos físicos relacionados con la presencia y flujo de cargas eléctricas. Se manifiesta en una gran variedad de fenómenos como los rayos, la electricidad estática, la inducción electromagnética o el flujo de corriente eléctrica.
. La electricidad es una forma de energía tan versátil que tiene un sinnúmero de aplicaciones, por ejemplo: transporte, climatización, iluminación y computación.
2.- CONCEPTOS BASICOS:
· Carga eléctrica: Esuna propiedad de algunas partículas subatómicas, que determina su interacción electromagnética. La materia eléctricamente cargada produce y es influida por los campos electromagnéticos.
· Corriente eléctrica: un flujo o desplazamiento de partículas cargadas eléctricamente por un material conductor; se mide en amperios.
· Campo eléctrico: Es un tipo de campo electromagnético producido por una carga eléctrica incluso cuando no se está moviendo. El campo eléctrico produce una fuerza en toda otra carga, menor cuanto mayor sea la distancia que separa las dos cargas. Además las cargas en movimiento producen campos magnéticos.
· Potencial eléctrico: Es la capacidad que tiene un campo eléctrico de realizar trabajo; se mide en voltios.
· Electromagnetismo: La corriente eléctrica produce campos magnéticos, y los campos magnéticos variables en el tiempo generan corriente eléctrica.
3.- PRINCIPALES LEYES EN ELECTRICIDAD:
. La ley de Ohm, postulada por el físico y matemático alemán Georg Simon Ohm, es una ley de la electricidad. Es una ley válida para los materiales "óhmicos" que son la mayoría de los empleados en componentes eléctricos (si bien existen tipos de materiales y dispositivos que no satisfacen la ley de Ohm).
. La ley establece que la diferencia de potencial V que aparece entre los extremos de un conductor determinado es proporcional a la intensidad de la corriente I que circula por el citado conductor. Ohm completó la ley introduciendo la noción de resistencia eléctrica R; que es el factor de proporcionalidad que aparece en la relación entre V e I:
EVALUACIÓN PERMANENTE 1 - Toma de decisiones
ALGORITMO
1.- CONCEPTO E IMPORTANCIA
. Es un conjunto de pasos lógicos y estructurados que nos permiten dar solución a un problema.
. La importancia de un algoritmo radica en desarrollar un
razonamiento lógico matemático a través de la comprensión y aplicación de
metodologías para la resolución de problemas.
ESTRUCTURA:
ESTRUCTURA:

. ENTRADA : Es la introducción de
datos para ser transformados.
. PROCESO : Es el conjunto de
operaciones a realizar para dar solución a un problema.
. SALIDA : Son los resultados obtenidos a
traves del proceso.
2.- DISEÑO DE ALGORITMOS
. 2.1 ALTERNATIVAS DE SOLUCION
Es la forma de representar la secuencia logica
de ejecución de instrucciones
Esta puede ser a traves de :
1).- DIAGRAMAS DE FLUJO
2).- PSEUDOCODIGO.
. 2.2 DIAGRAMAS DE FLUJO
Es empleado para representar la solución de
un algoritmo empleando figuras geométricas, donde cada una de ellas
representa en particular una tarea especifica que realizar.
Las mas comunes son:

. 2.2 PSEUDOCODIGO
Es empleado para representar la solución de un algoritmo empleando lenguaje natural escrito estableciendo la secuencia de pasos sin imprecisiones y de manera clara.

3- USO DE DIAGRAMA DE FLUJO, PSEUDOCODIGO PARA LOS TIPOS DE ESTRUCTURA
. 3.1 SECUENCIALES: Implica escribir una acción tras otra, donde la primera que se haya escrito es la primera que se ejecutara.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

. 3.2 SELECTIVAS:
Se usan para TOMAR DECISIONES.
- Simples: Lo que se hace es EVALUAR la condición, si la condición es verdadera se realiza la acción, en caso contrario termina el programa.
- Simples: Lo que se hace es EVALUAR la condición, si la condición es verdadera se realiza la acción, en caso contrario termina el programa.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

- Dobles: Luego de evaluar una condición si esta se
cumple, es decir si es verdadera realiza una serie de acciones, y si esta es
falsa se realiza otra serie de acciones distinta a la primera.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

- Multiples: Se realiza a partir de anidar estructuras
simples y/o dobles de manera que se realicen diferentes acciones con base a
varias comparaciones, así habrá tantas opciones como se
requieran.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

. 3.2 REPETITIVAS: Este
tipo de estructura se utilizan para ejecutar acciones repetidamente, esto se
hace posible mediante una secuencia de instrucciones que se repiten una y otra
vez y así evitamos escribir múltiples veces las instrucciones.
- PARA: Esta estructura ejecuta los pasos de la
solución del algoritmo un número definido de veces y de modo automático
controla el número de interacciones o pasos a través del cuerpo del
ciclo. Para el control se utiliza un contador en el cual se va acumulando
el número de veces que se ha repetido las instrucciones.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

- MIENTRAS: Se utiliza cuando NO sabemos el numero de
veces que se ha de repetir un ciclo, los ciclos se determinar por una condición
que se evalúa al inicio del ciclo, es decir, antes de ejecutarse todos los
pasos.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

- HACER - MIENTRAS O REPETIR: En esta estructura el ciclo se va a repetir hasta que la condición se cumpla, a diferencia de las estructuras anteriores la condición se escribe al finalizar la estructura.

EJEMPLO:
Pseudocodigo

Diagrama De Flujo

BIBLIOGRAFÍA
1. Samperio Monroy Theira Irasema. Antología “Programación Estructurda”.
Diciembre 2013.
2. Cairó Olvaldo, Metodología de la programación (algoritmos, diagramas deflujo y
programas), Editorial Alfaomega, Segunda edición.
3. Joyanes Aguilar Luís, Fundamentos de programación (Algoritmos, estructuras de datos y
objetos), Editorial McGraw Hill, TerceraEdición.
4. Ferreyra Cortés Gonzalo, Informática para cursos de bachillerato, Editorial Alfaomega, Segunda Edición
5. Imágenes obtenidas del Software DFD y Pseint
isntalado en pc.
Suscribirse a:
Entradas (Atom)
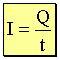
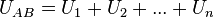



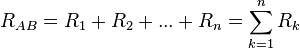
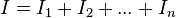


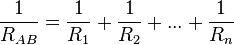








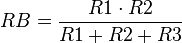






 o también
o también 












